This post is in regards higher dimensional partial integration, a topic of vector calculus. Here I show a quick and non-formal way of integrating by parts in higher dimensions.
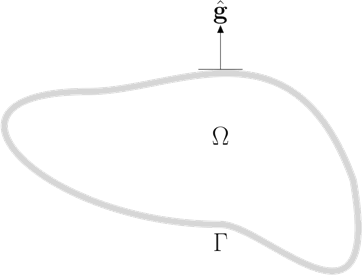
Consider the volume integration over omega which is bounded by the manifold gamma. Omega is assumed an open bounded subset of R^n, and gamma assumed a piecewise smooth boundary. These assumptions are required by Stoke's theorem.
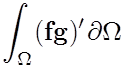
First apply the product rule under the integral.
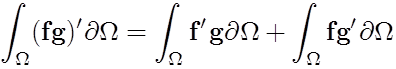
Second, use Stoke's theorem to evaluate the volume integral
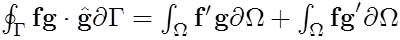
Here, the surface integral is projected against the outward facing normal, g-hat. The right hand side remains unchanged. Simply re-arrange to get:
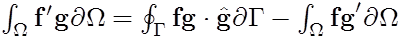
As a matter of notation, let
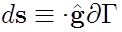
To arrive at
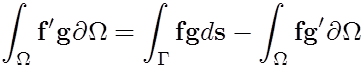
I find it interesting to look at the case where omega is one dimensional, as the above expression quickly collapses down to the more well know expression of partial integration:
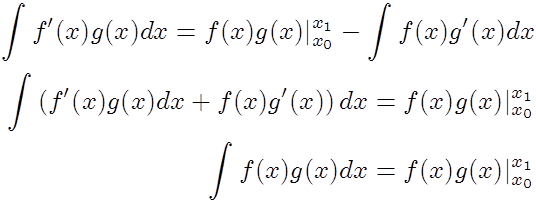
The justification of "left minus right" on the right had side's evaluation is now seen as a result of the outward facing normals at the evaluation points x_0 and x_1.